Jan 2024 Update: Drag the appropriate labels to their respective targets.

Question

Drag the appropriate labels to their respective targets.

Asked By CrystalCove96 at 30 Jan 2024

Answered By Expert

Timothy

Expert · 4.8k answers · 4k people helped

Step 1/2

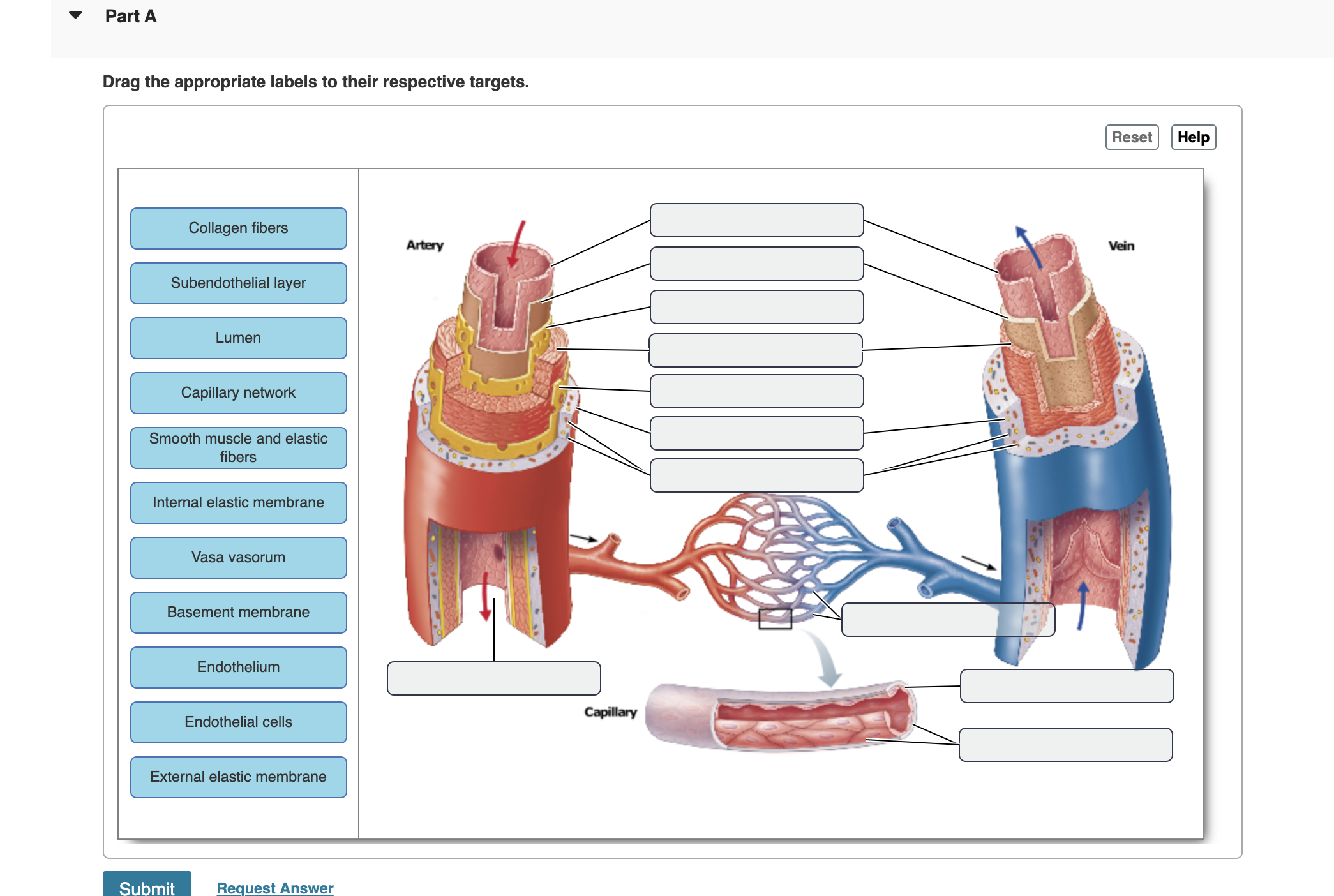
The given figure is of the blood vessels with their microscopic layers.

Starting from the major vessels the artery and the vein.

From above to downwards.

1)Endothelium

2)Subendothelial Membrane

3)Internal Elastic Membrane (not present in vein)

4)Smooth Muscle and elastic fibres

5)External Elastic Membrane (not present in vein)

6)Collagen Fibres

7) Vasa vasorum

8)Lumen(on the left)

Under a broad spectrum understanding the structure of vessels

Explanation:

Arterial Walls:

Explanation:

Venous Walls:

Explanation:

Step 2/2

Furthermore

The labellings for capillary are:

1) Capillary network

2)Basement Membrane

3)Endothelial Cells

Explanation:

Capillaries are the smallest and thinnest blood vessels in the human body, designed for the exchange of oxygen, nutrients, and waste products between the blood and tissues. Despite their small size, capillaries have a unique and specialized wall structure:

Explanation:

Final Answer

Final Answer ➡️

ℹ️From above to downwards.

1)Endothelium

2)Subendothelial Membrane

3)Internal Elastic Membrane (not present in vein)

4)Smooth Muscle and elastic fibres

5)External Elastic Membrane (not present in vein)

6)Collagen Fibres

7) Vasa vasorum

8)Lumen(on the left)

ℹ️for capillary :

1) Capillary network

2)Basement Membrane

3)Endothelial Cells

🧑‍🏫 More Questions

Which of the following is an ethmoid bone feature? Multiple Choice Sella turcica Mental foramen Cribriform plate Jugular foramen SP 2 o 3 ch

1. [9 pts] Consider the Hermiticity of the following operators: (a) Is the operator dxd a Hermitian operator? Prove your answer (b) Is the operator dx2d2 a Hermitian operator? Prove your answer. (c) Is the Hamiltonian operator H<svg xmlns="http://www.w3.org/2000/svg" width='100%' height='0.24em' viewBox='0 0 1062 239' preserveAspectRatio='none'><path d='M529 0h5l519 115c5 1 9 5 9 10 0 1-1 2-1 3l-4 22 c-1 5-5 9-11 9h-2L532 67 19 159h-2c-5 0-9-4-11-9l-5-22c-1-6 2-12 8-13z'/></svg>=−2mℏ2dx2d2+V(x) a Hermitian operator if V(x) is a real-valued function? Prove your answer . Hints: For (a) and (b), you may want to use integration by parts, and you may presume that any well-behaved function Ψ(x) and its derivative dxdΨ(x) vanish at ±∞.

Check the functions of connective tissue. Supporting the internal frame of the body Energy storage Hormone transport Protecting the vital organs Forming the structural framework of the liver

Which of the following statements best describes sexual selection? Sexual selection occurs when there is a difference in mating success among individuals of the same sex with different phenotypes. Sexual selection acts only on traits related to finding a mate. Sexual selection refers to selection for ornamentation traits in males that help them acquire mates. Sexual selection applies only to males.

Problem 5 (3 pts) Prove for positive a, b the equality ab a dc = dr + х X X

👉 Interested in exploring further?

Chrome Extension

1. Search answers from our 90+ million questions database.

2. Get instantly AI Solutions powered by most advanced models like GPT-4, Bard, Math GPT, etc.

3. Enjoy one-stop access to millions of textbook solutions.

4. Chat with 50+ AI study mates to get personalized course studies.

5. Ask your questions simply with texts or screenshots everywhere.

Get It

Compare

Legal