Blue Raider Adventure Park ACTG 2110 - Principles of Accounting Accounting Cycle Packet Serial Problem Covering Chapters 2-4 (Spring 2020) INTRODUCTION: Matt Lapinski, an MTSU student, consistently encounters problems balancing his work life and his academic life. Matt's employer complains about rearranging the company's work schedule every semester to accommodate Matt's new class schedule. Also, Matt frequently feels pressure to work more hours than he can manage while simultaneously working up to his full potential at school. Matt decides that starting his own business will enable him to have more control over his work schedule. In addition, this short-term business venture will provide him with some valuable business experience to include on his resume. Matt needs to find a business venture that requires a minimum amount of capital investment because he, like most college students, doesn't have much cash to invest. He also feels he would be more motivated to put in the hard work that it takes to build a successful business if it involves some activity that he enjoys. After careful consideration, Matt decides to establish Blue Raider Adventure Park on some land his grandfather owns (and has agreed to let Matt use for free!) just outside the city limits of Murfreesboro. Matt has very fond childhood memories of countless hours spent playing on this land, so he decides to develop the adventure park to be of interest to school-age children. His grandfather's land had several natural features that offer the prospect of fun for children with minimal investment - a large pond for canoeing and a sizeable cave for spelunking tours. A long, winding nature trail can be developed for practically no cost. He plans to enhance the natural features of the land by developing an obstacle course and a ziplining course. A small, empty barn on the property will serve as both a ticket office and a storage building for the equipment. Matt is a business major who has not yet taken his first accounting course, so he is relying on you to help him properly account for his new business venture. Together you two decide to organize his business as a sole proprietorship based on his need to set up this business simply and economically. Matt begins developing the park in August, and he opens to the public on September 1. September 30 is Blue Raider Adventure Park's fiscal year end.
ne accounting cycle illustrated below is designed to provide information about a company's profitability (or lack thereofl) along with many other important financial characteristics. This same accounting cycle is applicable to businesses of any size - from small, local businesses like Blue Raider Adventure Park to large, global businesses like McDonalds: 3. Analyze transactions Joumalize Prepare unadjusted trial balance 10. Reverse Optional Accounting -Cycle Adjust Prepare post- closing trial balance Close Prepare statements Prepare adjusted trial balance Exhibit 4.7 - Steps in the Accounting Cycle (from Chapter 4 of your textbook) Each of these steps is explained in detail in Chapters 1-4 of our textbook. Step 1, Analyze transactions, is covered in Chapter 1. While this step is very important, it is a thought process, the results of which do not materialize into any written action until Step 2, Journalize. Therefore, we will begin this packet with Step 2 in our quest to complete the first full accounting cycle for Blue Raider Adventure Park The remaining pages of this packet guide you through this process to enhance your understanding of the complete accounting cycle as it relates to one business venture. This is a serial problem that will be completed over the span of three chapters - chapters 2, 3, and 4. Note that we provide "Helpful Hints" for each accounting cycle step based on our experience teaching this material to introductory accounting students. Several of these "Helpful Hints" include check figures which effectively allow you, to a great extent, to check your work for accuracy. In the event that your work does not reconcile with the check figure(s) provided, our expectation is that you will seek assistance, exhausting all available resources (including the Accounting Lab tutors (N428) and your professor), to correct your work before coming to class. Blue Raider Adventure Park's complete chart of accounts is listed on the following page. It too, includes helpful hints to ensure you understand that document. Please complete the various steps in this packet as directed by your professor.
Blue Raider Adventure Park Chart of Accounts Account Title Account Number 101 106 126 128 163 164 165 166 167 168 201 210 236 240 275 301 302 403 612 625 632 640 653 670 Cash Accounts Receivable Supplies Prepaid Insurance Equipment Accumulated Depreciation - Equipment Sign Accumulated Depreciation - Sign Activity Courses Accumulated Depreciation - Activity Courses Accounts Payable Wages Payable Unearned Revenue Interest Payable Notes Payable M. Lapinski, Capital M. Lapinski, Withdrawals Ticket Revenue Advertising Expense Depreciation Expense Insurance Expense Interest Expense Mowing Expense Supplies Expense Wages Expense Income Summary 682 999 Helpful Hints The Chart of Accounts is a list of all of the company's accounts and the number assigned to each account. The accounts will appear in this same order in the general ledger
Chapter 2 (Accounting Cycle Steps 2, 3, & 4) G CYCLE STEP 2: Journalize each of the following Blue Raider Adventure Park (BRAP) ons in the general journal; you may omit explanations. Use the general journal working papers in your packet. August 1 Matt opens a business checking account in the name of BRAP and makes an initial deposit of $7,000. Matt had previously withdrawn this $7.000 from his personal savings account. August 1 Matt is unable to borrow money from the local bank given his youth, lack of business experience, and lack of a substantial credit history. However, his grandfather fully supports Matt's efforts to become an entrepreneur, so he loans Matt $10,000 at 6% interest to be repaid in two years. Matt deposits these funds into the BRAP checking account. August 7 Matt goes to Play It Again Sports and pays $2,100 to purchase gently used canoes, paddles, lifejackets, ziplining harnesses, etc. to be used the park. (These items will collectively be identified as "Equipment" in the accounting records.) August 15 Matt purchases a large, attractive sign for the new park at a cost of $650. The sign maker knows Matt's family, so she agrees to extend credit to BRAP for 30 days. August 20 BRAP pays $250 to create, print, and distribute flyers to all the local schools and youth organizations to advertise that the new park will open on September 1. August 28 BRAP pays a total of $5,650 to have the child-appropriate obstacle and zipline courses constructed that same day; inspection and certification are included in these amounts. (These two courses will collectively be identified as "Activity Courses" in the accounting records.) September 1 Matt recognizes the fact that he could be sued if a child gets hurt in the park, so BRAP pays $660 to purchase 4 months of general liability insurance for coverage from September 1 through December 31. September 7 Matt establishes a 30-day credit account at a local business on behalf of BRAP. He immediately uses the account to purchase $420 in various supplies for the park. September 10 BRAP sells 60 tickets for $15 each to local school children for admission to the park on that same day. (All ticket sales by BRAP are cash sales unless otherwise noted.) September 14 BRAP pays for the sign purchased on August 15. September 17 The Boys and Girls Club of Rutherford County brings 90 disadvantaged children to BRAP. Matt agrees to accept a reduced price of $11.00 per ticket and wait 30 days to receive payment, which will be paid by the Club rather than by the children. September 18 | BRAP pays $60 to have the grass mowed at the park. September 22 BRAP sells 45 tickets for $15 each for children in two local Boy Scout troops for admission to the park on that same day. September 24 BRAP receives a check from the Boys and Girls Club of Rutherford County in the amount of $325 to partially pay for the tickets purchased on September 17. September 25 BRAP pays wages in the amount of $380 to two of Matt's friends who worked on days when children were in the park to assist the children with the various activities. September 28 Matt is satisfied that BRAP has more than a sufficient amount of operating cash in its checking account, so he writes himself a company check for $700 and deposits it into his own personal checking account. September 30 BRAP receives a check in the amount of $360 from Ms. Hughes, a local teacher, to purchase tickets for her 2nd graders. She plans to bring them to BRAP for a field trip on October 3. Helpful Hints Journalizing is the process of recording each transaction in the general journal in chronological (date) order using appropriate account titles and properly characterizing the increase or decrease to each account as either a debit or a credit, based on the account's normal balance. Debit lines are listed first, credits account titles are slightly indented, and DEBIT AMOUNTS MUST EQUAL CREDIT AMOUNTS for each and every individual transaction.
ACCOUNTING CYCLE STEP 3: Post each transaction in the general journal to the general ledger. Use the general ledger working papers provided in your packet. Helpful Hints Posting is the process of transferring general journal entry information to the general ledger. Each number you post should be properly cross-referenced by: o recording the general journal page number (ex. GJ1, GJ2, etc.) in the Posting Reference (Post. Ref.) column of the general ledger (transaction descriptions in the "Item" column may be eliminated", AND o recording the general ledger account number in the Post. Ref. column of the general journal. ACCOUNTING CYCLE STEP 4: Calculate the ending balance in each general ledger account if you haven't already done so, and prepare an unadjusted trial balance. No working papers have been provided for this step, so you may either handwrite your solution or prepare it electronically. If you prepare your solution electronically, be sure to bring a hardcopy to class. Helpful Hints Determine the balance in each account by subtracting the sum of the debits from the sum of the credits. The resulting difference (the updated account balance) is a debit if the sum of the debits is greater than the sur credits. Alternatively, the resulting difference (the updated account balance) is a credit if the sum of the credits is greater than the sum of the debits. Prepare an unadjusted trial balance by listing each general ledger account title with its balance in the order that it appears in the general ledger) according to the format presented in Exhibit 2.14 in your textbook. Note that the debit and credit columns must each be summed, and the sums must be equal. If debits do not equal credits, refer to the "Searching for and Correcting Errors" section in Chapter 2 of your textbook for additional assistance. Check Figure: Debits and credits must each equal $20,345.
Chapter 3 (Accounting Cycle Steps 5, 6, & 7) ACCOUNTING CYCLE STEP 5: Adjust the appropriate accounts of BRAP based on the following information. This step involves journalizing the adjusting entries in the general journal and posting them to the general ledger, using the cross-reference procedure described in accounting cycle step 3. (Note: Add these transactions to the general journal and general ledger that you began in the Chapter 2 section of this packet.) September 30 | One month of the general liability insurance coverage that began on September 1 has now expired. September 30 Accrue interest on the $10,000, 6% loan issued on August 1 even though payment on the principal and interest will not be made until the note matures in two years. (Round to the nearest dollar, if necessary.) September 30 Matt determined that $132 of the supplies purchased on September 7 remained unused. September 30 You consult with a fellow student who has already completed ACTG 2110, and he helps you calculate depreciation as follows: Equipment - $36; Sign - $12, and Activity Courses - $100. (Note: use separate Accumulated Depreciation accounts for each asset, but report the total amount of Depreciation Expense in a single account.) September 30 Accrue wages of $150. The employees earned these wages in September, but will not be paid until October Helpful Hints While there are no source documents to prompt us to record adjusting entries, adjusting entries are an important element of matching revenues and expenses to provide GAAP-compliant financial statements. Each adjusting entry affects an income statement account (revenue or expense) and a balance sheet account (asset or liability), so omitting an adjusting entry or making an error in the amount of the adjusting entry makes the income statement, the statement of owner's equity, and the balance sheet incorrect. Some helpful hints to keep in mind as you write adjusting entries: As previously noted, each adjusting entry affects an income statement account and a balance sheet account. No adjusting entry affects the Cash account.
*** ACCOUNTING CYCLE STEP 6: Recalculate the general ledger account balances for all accounts affected by the adjusting entries, if you haven't already done so, and then develop another trial balance consistent with the format of your unadiusted trial balance. This new trial balance is identified as an adjusted trial balance to reflect the fact that the account balances now include the effect of all adjusting entries. No workine papers have been provided for this step, so you may either handwrite your solution or prepare it electronically. If you prepare your solution electronically, be sure to bring a hardcopy to class. Helpful Hints Remember to list your accounts in financial statement order, just as you did for your unadjusted trial balance. Check Figure: Debits and credits must each equal $20,743. ACCOUNTING CYCLE STEP 7: Use the accounts and balances on the adjusted trial balance to prepare financial statements. Refer to Exhibit 3.14 in your textbook for an illustration of how the numbers from an adjusted trial balance flow to the financial statements. No working papers have been provided for this step, so you may either handwrite your solution or prepare it electronically. If you prepare your solution electronically, be sure to bring a hardcopy to class. Helpful Hints The income statement is always prepared first because we need the output of the income statement (net income) to prepare the second financial statement, the statement of owner's equity. The statement of owner's equity must be prepared second because we need the output of the statement of owner's equity (the ending capital account balance) to prepare the third financial statement, the balance sheet. The fact that all three financial statements tie together in this way is referred to as articulation. Recall that the accounts on the adjusted trial balance are listed in financial statement order (assets, liabilities, owner's equity, revenues, and expenses), so the accounts you need for each statement are effectively grouped together. Each account is reported on only ONE financial statement. Specifically note the difference between the format of a trial balance and a balance sheet. Many beginning accounting students frequently confuse these two due to the naming similarity, but they are two very distinct documents! Check Figures: Net income = $1,024 Total Assets = $18,354
Chapter 4 (Accounting Cycle Steps 8 & 9) ACCOUNTING CYCLE STEP 8: Prepare journal entries to close all the temporary accounts. This s includes journalizing the closing entries in the general journal and posting them to the appropriate general ledger accounts, using the cross-reference procedure described in Step 3. Use the same general journal and general ledger that you used in the previous steps. Helpful Hints The temporary accounts to be closed are the revenue accounts, expense accounts, and the owner's withdrawal (a.k.a. drawing) account. Note that the owner's capital account before the closing process does not equal the ending owner's capital we reported on the statement of owner's equity and on the balance sheet. The closing process, when properly completed, will update the owner's capital account balance in the general ledger so that it reconciles with the ending owner's equity balance we reported on the financial statements. The closing process will also reduce all temporary accounts to a zero balance clearing the way for the accumulation of revenues, expenses, and withdrawals for the next accounting period. Revenue accounts must be DEBITED to remove their credit balances and expense accounts and the owner's withdrawal account must be CREDITED to remove their debit balances. ACCOUNTING CYCLE STEP 9: Prepare a post-closing trial balance. Just like the unadjusted trial balance and the adjusted trial balance, this trial balance is simply a listing of the general ledger accounts and their balances in financial statement order with the debit and credit columns summed. See Exhibit 4.6 in your textbook for an example of a post-closing trial balance. No working papers been provided for this step, so you may either handwrite your solution or prepare it electronically. If you prepare your solution electronically, be sure to bring a hardcopy to class Helpful Hints This trial balance confirms that general ledger debits and credits are equal before beginning a new accounting cycle. Given that all the temporary account balances were reduced to zero during the closing process, the temporary accounts may be omitted from this trial balance. Check Figure: Debits and Credits must each equal $18,502. ACCOUNTING CYCLE STEP 10: Preparing reversing entries is an optional step in the accounting cycle that will not be covered in this course.
Page 1 Credit Debit Post. Ref. Blue Raider Adventure Park GENERAL JOURNAL Description Date -།་་ ་བ པ ་ བ ། = ཟ༢། བ བ = - ཟ7 ཟ| ༧ བ བ བ ན བ * - ཎ ཏཾ བ ར ༢
Blue Raider Adventure Park GENERAL LEDGER Account Cash Account No. 101 Date Balance Item Post. Ref Debit Credit Debit Credit
Account Accounts Receivable Account No. 106 Balance Debit Credit Date Item Post. Ref. Debit Credit Account Supplies Account No. 126 Balance Debit Credit Date Post. Ref. Item Debit Credit Account Prepaid Insurance Account No. 128 Date Item Post. Debit Credit Balance Ref Debit Debit Credit
Account Equipment Account No. 163 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Accumulated Depreciation Equipment Account No. 164 Balance Date Item Post Ref SE Debit Credit Debit Credit Account Sign Account No. 165 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Accumulated Depreciation - Sign Account No. 166 Balance Date Item Post. Ref. Debit Credit Debit Credit
Account Activity Courses Account No. 167 Date Item Balance Post. Ref. Debit Credit Debit Credit Account Accumulated Depreciation - Activity Courses Account No. 168 Date Balance Post. Item Debit Credit Ref. Debit Credit Account Accounts Payable Account No. 201 Balance Debit Credit Date Item Post. Ref. Debit Credit
Account Wages Payable Account No. 210 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Unearned Revenue Account No. 236 Post Balance Date Item Debit Credit Debit Credit Account Interest Payable Account No. 240 Post Balance Date Item Debit Credit Ref. Debit Credit Account Notes Payable Account No. 275 Date Item Post. Ref. Debit Credit Balance Debit Credit
count M. Lapinski, Capital Date Account No. 301 Balance Debit Credit Item Post. Debit Credit Ref. Account M. Lapinski, Withdrawals Account No. 302 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Ticket Revenue Account No. 403 Post. Balance Date Item Debit Credit Ref Debit Credit
Account Advertising Expense Account No. 612 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Depreciation Expense Account No. 625 Balance Date Item Post. Ref. Debit Credit Debit Credit Account Insurance Expense Account No. 632 Balance Debit Credit Date Item Post. Ref. Debit Credit LIITTI
Account Interest Expense Account No. 640 Balance Debit Credit Date Item Post. Ref. Debit Credit Account Mowing Expense Account No. 653 Balance Date Item Post. Ref. Debit Credit Debit Credit IIIII Account Supplies Expense Account No. 670 Balance Debit Credit Date Post. Ref. Item Debit Credit Account Wages Expense Account No. 682 Date Post. Ref. Item Debit Balance Credit Debit Credit
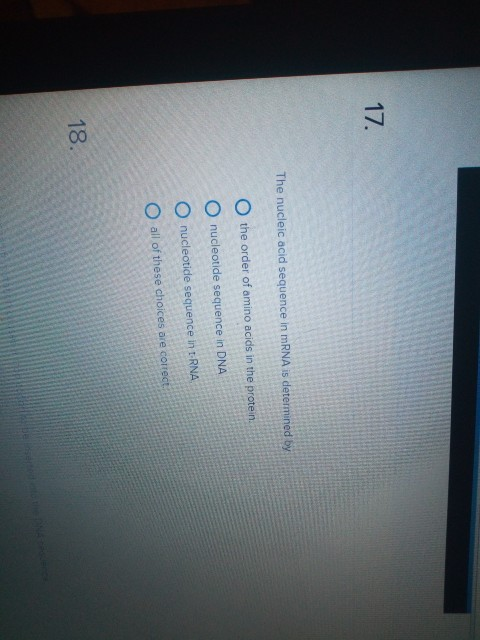
Account Income Summary Account No. 999 Date Balance Item Post. Ref. Debit Credit Debit Credit