🎁BACK-TO-SCHOOL DEAL. Subscribe Now to get 40% OFF at only 8.49 USD/month, only valid until Sep 30th, 2024

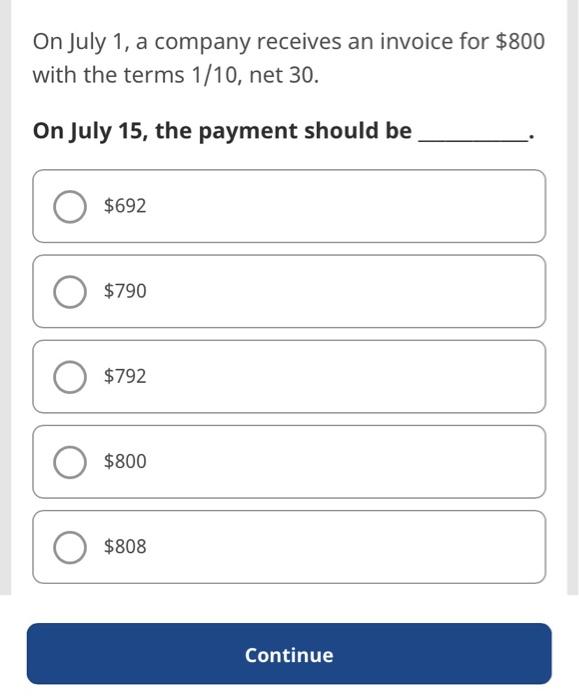
Question

Question
On July 1, a company receives an invoice for $800 with the terms 1/10, net 30. On July 15, the payment should be $692 $790 $792 $800 $808 Continue

Asked By TwilightGlider39 at

Answered By Expert

Bobby

Expert · 4.3k answers · 4k people helped

Sign in to see the answer

Step 1/1

ANSWER IS AS!

Q1)

A1)

Explanation:

The terms "1/10, net 30" mean that the buyer can take a 1% discount on the invoice price if the payment is made within 10 days; otherwise, the net amount of $800 is due within 30 days.

In this case, the payment amount with the 1% discount would be:

`\[ \$800 \times 0.99 = \$792 ]`

So, on July 15, the payment should be $792.

Final Answer

The final answer is as !

So, on July `15 ` , the payment should be ` $792.`

🧑‍🏫 More Questions

QUESTION 17/17 Your internet is out, and devices connected by WiFi and ethernet will not connect. You check several websites, and all your packets fail. You then ping a website with an IP address, and to your surprise, it's a success. Which would you do next? Open the DNS settings on your router and try using a different DNS Open the DHCP settings on your router and try using a different pool of private IP addresses Open the Port Forwarding settings on your router and try turning on UPnP Open the Network settings on your router and try adjusting the default gateway Open the Network settings on your router and try turning off your firewall

LAB REPORT SHEET 34 Peptides and Proteins A. Peptides 1. Condensed structural formulas of glycine and serine Glycine Serine DH 1 0 11 1 (H₂ H₃NT CH 0 11 (-0- H₂Nt - (H₂-C-0- 2. Condensed structural formulas of dipeptides Glycylserine Serylglycine 0 0 NH3 H3 Nt - (H3 -C-NH-CH-C-0- HO-CH2-CH-C-N- (Hz-170- 0 (H₂-OH H-2-0- 3. Condensed structural formulas of the reactants and products for the hydroly- sis of serylglycine 0 tt NH3 H3N+-1H-1-0- HO-CH₂-CH-I-N-C-0- Ін 11 OP (-N1-0-Ho CH OH H₂N+- (H₂-6-0- 4. Condensed structural formula for the tripeptide 5. Abbreviations for this tripeptide 3-letter abbreviation 1-letter abbreviation

<div><p>A medical record is an example of: Private behavior Public information Public behavior Private information</p></div>

Which of the statements best describe spongy bone? Spongy bone is softer than compact bone. Spongy bone is composed of branches of trabeculae. Spongy bone is lighter in weight than compact bone. Spongy bone receives nutrients through osteons.

Portia needs to create an invoice in QuickBooks. Which menu should she use? Income Expenses Reports Sales